降维

  • ravel()：如果没有必要，不会产生源数据的副本
  • flatten()：返回源数据的副本
  • squeeze()：只能对维数为1的维度降维
  • logspace 用于创建等比数列

假如，我们想要改变基数，不让它以10为底数，我们可以改变base参数，将其设置为2试试。

1
2
3
a = np.logspace(0,9,10,base=2)
a
array([   1.,    2.,    4.,    8.,   16.,   32.,   64.,  128.,  256.,  512.])

np.set_printoptions

1
np.set_printoptions(precision=None, threshold=None, edgeitems=None, linewidth=None, suppress=None, nanstr=None, infstr=None)

precision :

　　int, optional，float输出的精度，即小数点后维数，默认8（ Number of digits of precision for floating point output (default 8)）

threshold :

　　int, optional，当数组数目过大时，设置显示几个数字，其余用省略号（Total number of array elements which trigger summarization rather than full repr (default 1000).）

edgeitems :

　　 int, optional，边缘数目（Number of array items in summary at beginning and end of each dimension (default 3)）.

linewidth :

　　 int, optional，线条宽度 The number of characters per line for the purpose of inserting line breaks (default 75).

suppress :

　　 bool, optional，是否压缩由科学计数法表示的浮点数（Whether or not suppress printing of small floating point values using scientific notation (default False).）

nanstr :

　　 str, optional，String representation of floating point not-a-number (default nan).

infstr :

　　str, optional，String representation of floating point infinity (default inf).

bicount

1
2
3
4
5
6
7
8
9
10
# 找到一个数组中最常出现的数字
z = np.random.randint(0,10,50)
np.set_printoptions(threshold=1000)
print(z)
print(np.bincount(z))
print(np.argmax(np.bincount(z)))

[9 8 0 6 4 8 5 9 7 1 4 0 2 5 7 7 3 8 0 6 4 6 2 5 4 7 6 6 7 0 9 4 5 1 9 6 7 3 7 8 2 1 9 5 0 7 8 5 8 3]
[5 3 3 3 5 6 6 8 6 5]
7

其实bicount将结果映射成一个list，分别代表0出现的次数，1出现的次数。。。

找到出现最多次数的下标就是找到一个数组中最常出现的数字

lexsort

numpy.lexsort() 用于对多个序列进行排序。把它想象成对电子表格进行排序，每一列代表一个序列，排序时优先照顾靠后的列。

这里举一个应用场景：小升初考试，重点班录取学生按照总成绩录取。在总成绩相同时，数学成绩高的优先录取，在总成绩和数学成绩都相同时，按照英语成绩录取…… 这里，总成绩排在电子表格的最后一列，数学成绩在倒数第二列，英语成绩在倒数第三列。

练习题

Trick

1
2
3
4
5
6
np.add? # 显示帮助
np.add?? # 显示源代码
# fsting用法 python>=3.6
number = 7
f'My lucky number is {number}'

Matplotlib

  • %matplotlib inline: 这一句是IPython的魔法函数，可以在IPython编译器里直接使用，作用是内嵌画图，省略掉plt.show()这一步，直接显示图像。

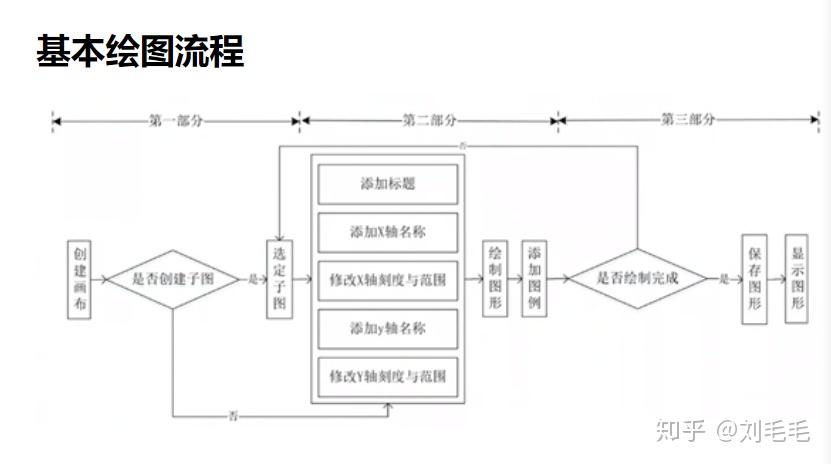
基本操作

  • 画图

    plt.plot(x,y)

  • 标签

    plt.xlabel('xlabel',fontsize = 16)

  • 线条&颜色

    字符 类型 字符 类型
    '-' 实线 '--' 虚线
    '-.' 虚点线 ':' 点线
    '.' 点 ',' 像素点
    'o' 圆点 'v' 下三角点
    '^' 上三角点 '<' 左三角点
    '>' 右三角点 '1' 下三叉点
    '2' 上三叉点 '3' 左三叉点
    '4' 右三叉点 's' 正方点
    'p' 五角点 '*' 星形点
    'h' 六边形点1 'H' 六边形点2
    '+' 加号点 'x' 乘号点
    'D' 实心菱形点 'd' 瘦菱形点
    '_' 横线点
    字符 颜色
    ‘b’ 蓝色，blue
    ‘g’ 绿色，green
    ‘r’ 红色，red
    ‘c’ 青色，cyan
    ‘m’ 品红，magenta
    ‘y’ 黄色，yellow
    ‘k’ 黑色，black
    ‘w’ 白色，white

  • 线条风格：

    plt.plot([1,2,3,4,5],[1,4,9,16,25],'-.',color='r')

    或者将两者结合使用

    plt.plot([1,2,3,4,5],[1,4,9,16,25],'ro')

  • 线宽 linewidth

    plt.plot(x,y,linewidth = 3.0)

  • 子图

    1
    2
    3
    4
    5
    6
    7
    # 211 表示一会要画的图是2行一列的 最后一个1表示的是子图当中的第1个图
    plt.subplot(211)
    plt.plot(x,y,color='r')

    # 212 表示一会要画的图是2行一列的 最后一个1表示的是子图当中的第2个图
    plt.subplot(212)
    plt.plot(x,y,color='b')

  • 标题

    plt.title('title')

  • 文本

    plt.text(x,y,'text)

    x,y为数轴上的坐标

  • 网格

    plt.grid(True)

  • 注释

    plt.annotate('tangyudi',xy=(-5,0),xytext=(-2,0.3),arrowprops = dict(facecolor='red',shrink=0.05,headlength= 20,headwidth = 20))

风格

  • 查看风格：

    plt.style.available

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    ['dark_background',
     'seaborn-talk',
     'seaborn-bright',
     'seaborn-ticks',
     'bmh',
     'ggplot',
     'seaborn-darkgrid',
     'classic',
     'fivethirtyeight',
     'seaborn-deep',
     'seaborn-colorblind',
     'seaborn-muted',
     'seaborn-pastel',
     'seaborn-notebook',
     'seaborn-paper',
     'seaborn-dark-palette',
     'seaborn-whitegrid',
     'seaborn-white',
     'grayscale',
     'seaborn-dark',
     'seaborn-poster']

  • 使用风格
    plt.style.use('ggplot')

    Parameters

    • style：str, dict, Path or list

      A style specification. Valid options are:

      • str: The name of a style or a path/URL to a style file. For a list of available style names, see style.available.

      • dict: Dictionary with valid key/value pairs for matplotlib.rcParams.

      • Path: A path-like object which is a path to a style file.

      • list: A list of style specifiers (str, Path or dict) applied from first to last in the list.

    1
    2
    3
    4
    5
    6
    7
    8
    import numpy as np
    import pandas as pd
    import matplotlib.pyplot as plt
    x = np.linspace(-10,10)
    y = np.sin(x)
    plt.style.use('ggplot')
    plt.plot(x,y)
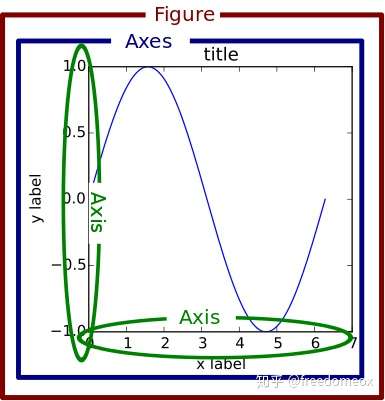
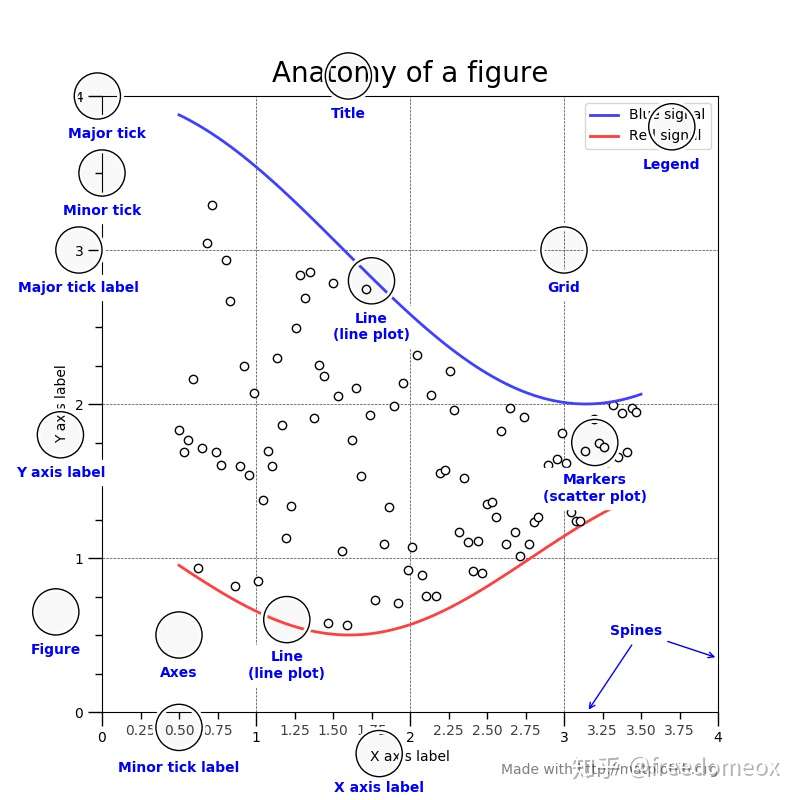
    plt.show()

面向对象画图

1
2
3
4
5
6
7
8
9
10
11
12
13
from matplotlib import pyplot as plt
x = np.arange(0, math.pi*2, 0.05)
y = np.sin(x)
#创建图形对象
fig = plt.figure()
#我们使用 add_axes() 将 axes 轴域添加到画布中
#add_axes() 的参数值是一个序列，序列中的 4 个数字分别对应图形的左侧开始画图位			置，底部开始画图位置，宽度缩放，和高度缩放，且每个数字必须介于 0 到 1 之间。
ax=fig.add_axes([0,0,1,1])
ax.plot(x,y)
ax.set_title("sine wave")
ax.set_xlabel('angle')
ax.set_ylabel('sine')
plt.show()
  • 图例

axes 类的 legend() 方法负责绘制画布中的图例，它需要三个参数，如下所示：

ax.legend(handles, labels, loc)

  • labels 是一个字符串序列，用来指定标签的名称；
  • loc 是指定图例位置的参数，其参数值可以用字符串或整数来表示；
  • handles 参数，它也是一个序列，它包含了所有线型的实例；

http://c.biancheng.net/matplotlib/

preview

https://zhuanlan.zhihu.com/p/139052035

img

img

https://zhuanlan.zhihu.com/p/93423829

结合pandas画图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
df=pandas.DataFrame()
常见的画图方法如下：
df.plot()
也可以传入参数：df.plot(kind=value)决定画什么类型的图
kind=line    画折线图
kind=bar     x轴画矩形图
kind=barh    y轴画矩形图
kind=pie     画饼图
kind=scatter 画散点
kind=box     画盒子图
kind=kde     画核密度估计图

或者:
df.plot.line()
df.plot.bar()
df.plot.barh()
df.plot.pie()
df.plot.scatter()
df.plot.box()
df.plot.kde()

sklearn

决策树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import numpy as np
import pandas as pd
from sklearn import tree
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
import graphviz
# pandas拼接数据
df = pd.concat([pd.DataFrame(wine.data), pd.DataFrame(wine.target)],axis=1)
# 划分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data, wine.target, test_size=0.3)
# 实例化一个分类器
clf = tree.DecisionTreeClassifier(criterion='entropy',random_state=3,splitter="random")
# 训练
clf = clf.fit(Xtrain, Ytrain)
# 评价结果
score = clf.score(Xtest, Ytest)


# 用graphviz画出决策树
dot_data = tree.export_graphviz(clf, feature_names=wine.feature_names, class_names=['0', '1', '2'], filled=True, rounded=True, special_characters=True)
graph = graphviz.Source(dot_data)
graph
# 确定最优剪枝参数
test = []
for i in range(10):
    clf = tree.DecisionTreeClassifier(criterion='entropy',random_state=30,
                                      splitter="random",
                                     max_depth=i+1,
                                     )
    clf = clf.fit(Xtrain, Ytrain)
    score = clf.score(Xtest, Ytest)
    test.append(score)

plt.plot(range(1,11), test, color='red', label='max_depth')
plt.legend()
plt.show()
# 网格搜索
# 使用网格搜索，能够帮助我们同时调整多个参数，采用枚举法
gini_thresholds = np.linspace(0,0.5,20)
entropy_thresholds = np.linspace(0,1,50)
parameters = {
    "criterion":('gini','entropy')
    ,"splitter":('best','random')
    ,'max_depth':[*range(1,11)]
    ,'min_samples_leaf':[*range(1,50,5)]
    ,'min_impurity_decrease':[*gini_thresholds]
    
}

clf = DecisionTreeClassifier(random_state=25)
GS = GridSearchCV(clf,parameters,cv=10)
GS.fit(Xtrain,Ytrain)

  • 特征重要性

clf.feature_importances_

[*zip(feature_name,clf.feature_importances_)]

  • Criterion这个参数正是用来决定不纯度的计算方法的。sklearn提供了两种选择：

1）输入”entropy“，使用信息熵（Entropy）

2）输入”gini“，使用基尼系数（Gini Impurity）

通常就使用基尼系数

数据维度很大，噪音很大时使用基尼系数

维度低，数据比较清晰的时候，信息熵和基尼系数没区别

当决策树的拟合程度不够的时候，使用信息熵

两个都试试，不好就换另外一个

  • random_state & splitter

random_state用来设置分枝中的随机模式的参数，默认None，在高维度时随机性会表现更明显，低维度的数据（比如鸢尾花数据集），随机性几乎不会显现。输入任意整数，会一直长出同一棵树，让模型稳定下来。

splitter也是用来控制决策树中的随机选项的，有两种输入值，输入”best”，决策树在分枝时虽然随机，但是还是会优先选择更重要的特征进行分枝（重要性可以通过属性feature_importances_查看），输入“random”，决策树在分枝时会更加随机，树会因为含有更多的不必要信息而更深更大，并因这些不必要信息而降低对训练集的拟合。这也是防止过拟合的一种方式。当你预测到你的模型会过拟合，用这两个参数来帮助你降低树建成之后过拟合的可能性。当然，树一旦建成，我们依然是使用剪枝参数来防止过拟合

剪枝策略

  • max_depth

​ 限制树的最大深度，超过设定深度的树枝全部剪掉

  • min_samples_leaf & min_samples_split

    min_samples_leaf限定，一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本，否则分枝就不会发生，或者，分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生。一般搭配max_depth使用，在回归树中有神奇的效果，可以让模型变得更加平滑。这个参数的数量设置得太小会引起过拟合，设置得太大就会阻止模型学习数据。一般来说，建议从=5开始使用。如果叶节点中含有的样本量变化很大，建议输入浮点数作为样本量的百分比来使用。同时，这个参数可以保证每个叶子的最小尺寸，可以在回归问题中避免低方差，过拟合的叶子节点出现。对于类别不多的分类问题，=1通常就是最佳选择。

    min_samples_split限定，一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝，否则分枝就不会发生。

回归树

1
2
3
4
5
import numpy as np
from sklearn.tree import DecisionTreeRegressor
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_1.fit(X, y)
y_1 = regr_1.predict(X_test)

随机森林

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

wine = load_wine()
wine.data
wine.target
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data,wine.target,test_size=0.3)

#clf = DecisionTreeClassifier(random_state=0)
rfc = RandomForestClassifier(random_state=0)
#clf = clf.fit(Xtrain,Ytrain)
rfc = rfc.fit(Xtrain,Ytrain)
#score_c = clf.score(Xtest,Ytest)
score_r = rfc.score(Xtest,Ytest)


#交叉验证：是数据集划分为n分，依次取每一份做测试集，每n-1份做训练集，多次训练模型以观测模型稳定性的方法

rfc_l = []
clf_l = []

for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    rfc_l.append(rfc_s)
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()
    clf_l.append(clf_s)
    
plt.plot(range(1,11),rfc_l,label = "Random Forest")
plt.plot(range(1,11),clf_l,label = "Decision Tree")
plt.legend()
plt.show()

#是否有注意到，单个决策树的波动轨迹和随机森林一致？
#再次验证了我们之前提到的，单个决策树的准确率越高，随机森林的准确率也会越高

  • 随机森林填充数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
X_missing_reg = X_missing.copy()
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values
for i in sortindex:
    
    #构建我们的新特征矩阵和新标签
    df = X_missing_reg
    fillc = df.iloc[:,i]
    df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
    
    #在新特征矩阵中，对含有缺失值的列，进行0的填补
    df_0 =SimpleImputer(missing_values=np.nan,
                        strategy='constant',fill_value=0).fit_transform(df)
    
    #找出我们的训练集和测试集
    Ytrain = fillc[fillc.notnull()]
    Ytest = fillc[fillc.isnull()]
    Xtrain = df_0[Ytrain.index,:]
    Xtest = df_0[Ytest.index,:]
    
    #用随机森林回归来填补缺失值
    rfc = RandomForestRegressor(n_estimators=100)
    rfc = rfc.fit(Xtrain, Ytrain)
    Ypredict = rfc.predict(Xtest)
    
    #将填补好的特征返回到我们的原始的特征矩阵中
    X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),X_missing_reg.columns[i]] = Ypredict
    # X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict 可能报错

预处理

方差过滤

比如一个特征本身的方差很小，就表示样本在这个特征上基本没有差异，可能特征中的大多数值都一样，甚至整个特征的取值都相同，那这个特征对于样本区分没有什么作用所以无论接下来的特征工程要做什么，都要优先消除方差为0的特征

1
2
3
4
5
6
7
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold() #实例化，不填参数默认方差为0
X_var0 = selector.fit_transform(X) #获取删除不合格特征之后的新特征矩阵
# 过滤一半的变量
import numpy as np
X_fsvar = VarianceThreshold(np.median(X.var().values)).fit_transform(X) X.var().values
np.median(X.var().values)

卡方过滤

专门针对离散型标签（即分类问题）的相关性过滤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
#假设在这里我一直我需要300个特征
X_fschi = SelectKBest(chi2, k=300).fit_transform(X_fsvar, y)
X_fschi.shape
cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()

chivalue, pvalues_chi = chi2(X_fsvar,y)
#k取多少？我们想要消除所有p值大于设定值，比如0.05或0.01的特征：
k = chivalue.shape[0] - (pvalues_chi > 0.05).sum()
X_fschi = SelectKBest(chi2, k=填写具体的k).fit_transform(X_fsvar, y)
cross_val_score(RFC(n_estimators=10,random_state=0),X_fschi,y,cv=5).mean()

F检验（只能检验线性关系）

它即可以做回归也可以做分类，因此包含feature_selection.f_classif（F检验分类）和feature_selection.f_regression（F检验回

归）两个类。其中F检验分类用于标签是离散型变量的数据，而F检验回归用于标签是连续型变量的数据

1
2
3
4
5
from sklearn.feature_selection import f_classif
F, pvalues_f = f_classif(X_fsvar,y) 
k = F.shape[0] - (pvalues_f > 0.05).sum()
X_fsF = SelectKBest(f_classif, k=填写具体的k).fit_transform(X_fsvar, y)
cross_val_score(RFC(n_estimators=10,random_state=0),X_fsF,y,cv=5).mean()

互信息法

特征工程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Normalization 归一化 一般来说将数据分部在0到1之间
from sklearn.preprocessing import MinMaxScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler = MinMaxScaler()
# scaler = MinMaxScaler(feature_range=[5,10])
result_ = scaler.fit_transform(data) #训练和导出结果一步达成


# sklearn 里面处理标准化这些需要二维数组
# Standardization 标准化 将数据处理成标准正态分布形式
from sklearn.preprocessing import StandardScaler
data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
scaler = StandardScaler() #实例化
res = scaler.fit_transform(data) #使用fit_transform(data)一步达成结果
res.mean()
res.std()

数据预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# sklearn 里面处理标准化这些需要二维数组
shape(-1,1) # 变成一列
shape(1,-1) # 变成一行

# 如果数据自带索引，导入时需指定索引列
import pandas as pd
data = pd.read_csv(r"C:\work\learnbetter\micro-class\week 3 Preprocessing\Narrativedata.csv",index_col=0)

# 缺失数据处理
import pandas as pd
data = pd.read_csv(r"C:\work\learnbetter\micro-class\week 3 
Preprocessing\Narrativedata.csv",index_col=0)
data.head()
data.loc[:,"Age"] = data.loc[:,"Age"].fillna(data.loc[:,"Age"].median())
#.fillna 在DataFrame里面直接进行填补
data.dropna(axis=0,inplace=True)
#.dropna(axis=0)删除所有有缺失值的行，.dropna(axis=1)删除所有有缺失值的列
#参数inplace，为True表示在原数据集上进行修改，为False表示生成一个复制对象，不修改原数据，默认False
                   
                   
# sklearn只能处理数值型数据，因此要将标签转为数据
from sklearn.preprocessing import LabelEncoder
y = data.iloc[:,-1] #要输入的是标签，不是特征矩阵，所以允许一维
le = LabelEncoder() #实例化
label=le.fit_transform(y)
data.iloc[:,-1] = label #让标签等于我们运行出来的结果

逻辑回归

Perceptrons

参数名称 参数取值 参数解释
penalty 默认=None，即不加惩罚项，‘l2’（L2正则） or ‘l1’（L1正则） or ‘elasticnet’（混合正则） 惩罚项，加上惩罚项主要为了避免模型过拟合风险
alpha 默认=0.0001，取值为浮点数 如果penalty不为None，则正则化项需要乘上这个数
l1_ratio 默认=0.15，取值在[0,1] 一般只在penalty=elasticnet时用，当l1_ratio =0就是L2正则，当l1_ratio =1就是L1正则，当在(0,1)之间就是混合正则
fit_intercept bool值，默认=True 是否对参数 截距项b进行估计，若为False则数据应是中心化的
max_iter int整数，默认=1000 最大迭代次数，哪怕损失函数依旧大于0/
tol float or None，默认=10^(-3) 迭代停止的标准。如果不为None，那么当loss-pre-loss<tol的时候，就会停止迭代。因为当前迭代造成的损失函数下降太小了，迭代下去对loss影响不大了。
shuffle bool值，默认=True 每轮训练后是否打乱数据
verbose 取值为整数，默认=0 verbose = 0 为不在标准输出流输出日志信息，verbose = 1 为输出进度条记录；verbose = 2 为每个epoch输出一行记录
eta0 取值双精度浮点型double，默认=1 学习率，决定梯度下降时每次参数变化的幅度
n_jobs 取值为 int or None，默认=None 在多分类时使用的CPU数量，默认为None（或1），若为-1则使用所有CPU
random_state 取值为int, RandomState instance or None，默认=None 当 shuffle =True时，用于打乱训练数据
n_iter_no_change 取值int，默认=5 在提前停止之前等待验证分数无改进的迭代次数，用于提前停止迭代
early_stopping 取值bool值，默认=False 当验证得分不再提高时是否设置提前停止来终止训练。若设置此项，当验证得分在n_iter_no_change轮内没有提升时提前停止训练
class_weight 取值为dict, {class_label: weight} 或者 “balanced”或者None，默认=None 用于拟合参数时，每一类的权重是多少。当为None时，所有类的权重为1，等权重；当为balanced时，某类的权重为该类频数的反比，当为字典时，则key为类的标签，值为对应的权重
warm_start 取值为bool，默认=False 若为True则调用前一次设置的参数，使用新设置的参数

  • eta0 学习率

    类似于步长，步长太小收敛太慢，步长太长，反复横跳，无法收敛。

LogisticRegression

  • penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。

  • dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。

  • tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。

  • c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。

  • fit_intercept：是否存在截距或偏差，bool类型，默认为True。

  • intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。

  • class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。举个例子，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。当class_weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。
    那么class_weight有什么作用呢？

    在分类模型中，我们经常会遇到两类问题：
    第一种是误分类的代价很高。比如对合法用户和非法用户进行分类，将非法用户分类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以适当提高非法用户的权重。
    第二种是样本是高度失衡的，比如我们有合法用户和非法用户的二元样本数据10000条，里面合法用户有9995条，非法用户只有5条，如果我们不考虑权重，则我们可以将所有的测试集都预测为合法用户，这样预测准确率理论上有99.95%，但是却没有任何意义。这时，我们可以选择balanced，让类库自动提高非法用户样本的权重。提高了某种分类的权重，相比不考虑权重，会有更多的样本分类划分到高权重的类别，从而可以解决上面两类问题。

  • random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。

  • solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：

  • liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。

  • lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

  • newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

  • sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

  • saga：线性收敛的随机优化算法的的变重。

总结：
liblinear适用于小数据集，而sag和saga适用于大数据集因为速度更快。
对于多分类问题，只有newton-cg,sag,saga和lbfgs能够处理多项损失，而liblinear受限于一对剩余(OvR)。啥意思，就是用liblinear的时候，如果是多分类问题，得先把一种类别作为一个类别，剩余的所有类别作为另外一个类别。一次类推，遍历所有类别，进行分类。
newton-cg,sag和lbfgs这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear和saga通吃L1正则化和L2正则化。
同时，sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。
从上面的描述，大家可能觉得，既然newton-cg, lbfgs和sag这么多限制，如果不是大样本，我们选择liblinear不就行了嘛！错，因为liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR，不支持MvM，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
max_iter：算法收敛最大迭代次数，int类型，默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用，算法收敛的最大迭代次数。

  • multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。

  • OvR和MvM有什么不同？
    OvR的思想很简单，无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
    而MvM则相对复杂，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。
    可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而MvM分类相对精确，但是分类速度没有OvR快。如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。

  • verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。

  • warm_start：热启动参数，bool类型。默认为False。如果为True，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。

  • n_jobs：并行数。int类型，默认为1。1的时候，用CPU的一个内核运行程序，2的时候，用CPU的2个内核运行程序。为-1的时候，用所有CPU的内核运行程序。

做题遇到的

数据格式化map

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 将 df2 的获奖时间格式化为 x月x日
def time_format(x):
    
    return x.strftime("%m月%d日")

df2['获奖时间'] = df2['获奖时间'].map(time_format)
# 等同于
df2.获奖时间.map(lambda x: x.strftime('%m月%d日'))


def turn_percentage(x):
    return '%F.2f%%' % (x * 100);
  
  

q1_df['AT_HOME']=q1_df['AT_HOME'].apply(turn_percentage)
q1_df['AT_HOME']=q1_df['AT_HOME'].map(lambda x: "{:.2%}".format(x))

# 显示小数
pd.set_option('precision', 2)

# map传字典
df1['A'] = df1['A'].map({'A0':'cat','A3':'rabbit'})

# map ignore
df1['B'] = df1['B'].map(lambda x:f'{x} 今天关注了早起Python', na_action='ignore')

#applymap可以对整个 dataframe 工作，现在将 df1 的最后三列保留两位小数

df1[['D','E','F']] = df1[['D','E','F']].applymap(lambda x:format(x,'.2f'))


索引

  • reset_index用于将索引还原成默认值，即从0开始步长为1的数组。
1
2
3
4
5
6
7
8
9
q1_df['rate'] = [x for x in range(1,len(q1_df['AT_HOME'])+1)]
# 如果索引不是默认
q1_df.reset_index().set_index(q1_df['rate'])
# 如果是默认
q1_df.set_index(q1_df['rate'],inplace=True)
# 删除索引
max_data=max_data.reset_index(drop=True).set_index(max_data['DATA_DATE'])
# 修改索引名
df.rename_axis(["行政区", "公司规模"],inplace=True)

坐标轴显示百分比

  • 第一种方法
1
2
3
4
from matplotlib.ticker import FuncFormatter
def to_percent(temp, position):
    return '%1.0f'%(100*temp) + '%'
plt.gca().yaxis.set_major_formatter(FuncFormatter(to_percent))
  • 推荐
1
ax.set_yticklabels(['0%','10%','20%','30%','40%','50%'])

apply

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 构建apply函数
def judge_state(row):
    if row['Austin - EV'] <=0.01:
        return 'Off'
    elif row['Austin - EV']>0.01:
        return 'On'
# 应用apply函数
df_Austin_ev = df.apply(judge_state,axis = 1)

# 保留2位小数，如23.12%
def turn_percentage(x):
    return '%.2f%%' % (x * 100)
# 应用自定义函数
ratio=ratio['Austin - EV'].apply(turn_percentage)


# 我们将会用到 transform 而不是 apply。 原因是， transform 将会保持 dataframe 矩阵的形状(shape)(就是行列数不变)而 apply 会改变矩阵的形状。

重采样

1
2
# 重采样
df['购买月份'] = pd.to_datetime(df.日期).dt.to_period("M")

del

1
2
3
del df['a']
# 等价于
df.drop('a',axis=1,inplace=True)

按时间筛选

  • 第一种
1
2
3
4
5
6
# 将DateTime转成日期格式
df['DateTime'] = pd.to_datetime(df['DateTime'])
# 将日期设为index
df = df.set_index('DateTime')
# 筛选从2019年3月1号到2019年3月10号整十天的电网数据
df1 = df['2019-03-01':'2019-03-10']
  • 第二种
    1
    2
    3
    4
    5
    6
    # 设置开始时间
    from_date = df['DATA_DATE']>='2021-01-01'
    # 设置结束时间
    to_date = df['DATA_DATE']<='2021-03-31'
    # 筛选数据时间段
    df = df[from_date&to_date]

显示中文

1
2
3
4
5
6
7
# win设置中文
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

# mac设置中文
plt.rcParams['font.family'] = 'Heiti TC'#用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号

重命名

1
2
3
4
# 重命名 列
q4_df.rename(columns={'AT_HOME':'empty_ratio'},inplace=True)
# 重命名 索引
df.rename_axis("金牌排名",inplace=True)

填充

1
2
3
4
5
6
7
8
'''
bfill 从后面往前填充
ffill 从前往后
默认列方向填充0，1使用行方向
'''

# 新增一列 最多奖牌数量 列，值为该国 金、银、铜 牌数量中最多的一个奖牌数量
df['最多奖牌数量'] = df.bfill(1)[["金牌数", "银牌数",'铜牌数']].max(1)

查询

1
2
3
4
5
6
7
8
# 查询
df.query('金牌数+银牌数 > 15')

df[df.国家奥委会.str.contains('国')]

df_01.loc[df_01['行业（按行业大类）'].isin(['工业','建筑业'])]
df_01.loc[(df_01['行业（按行业大类）']=='工业')|(df_01['行业（按行业大类）']=='建筑业')]
df_01[df_01['行业（按行业大类）'].str.contains('工业|建筑业')]

选择类型

1
2
df4.select_dtypes(include=['int','float64'])
df4.select_dtypes(exclude=['int','float64'])

数据展开

1
df5.explode(['A','C'])

数据累加

1
2
df[list('ABCD')].cumsum()
df[list('ABCD')].cumsum(axis = 1)

列操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 插入列
tmp3 = (df['春节期间（除夕至初六）用电量']-df['节前温度接近的一周用电量'])/df['节前温度接近的一周用电量']
tmp1 = df.iloc[:,:1]
tmp2 = df.iloc[:,1:]
df = pd.concat([tmp1,tmp3.to_frame(),tmp2],axis=1,ignore_index=True)
df.columns=['a','b','c','d']
df
# 删除列
df.drop('rate',1)
# 新增列
df['比赛地点'] = '东京'
# 新增一列 最多奖牌数量 列，值为该国 金、银、铜 牌数量中最多的一个奖牌数量 例如美国银牌最多，则为41，中国为38 bfill默认跨行填充
df['最多奖牌数量'] = df.bfill(1)[["金牌数", "银牌数",'铜牌数']].max(1)
# 如果一个国家的金牌数大于 30 则值为 是，反之为 否
df['金牌大于30']  = np.where(df['金牌数'] > 30, '是', '否')
# 删除 df 的 7、8、9、10 列
df.drop(df.columns[[7,8,9,10]], axis=1,inplace=True)
# 提取第1，2，3，4列
df.iloc[:,0:4] 
df.iloc[:,[0,1,2,3]]
# 提取 金牌数、银牌数、铜牌数 三列
df[['金牌数','银牌数','铜牌数']]
# 提取全部列名中以 “数” 结尾的列
df.loc[:, df.columns.str.endswith('数')]


行操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# 插入行 先切分再插入
df1 = df.iloc[:1, :]
df2 = df.iloc[1:, :]
df3 = pd.DataFrame([[i for i in range(len(df.columns))]], columns=df.columns)
df_new = pd.concat([df1, df3, df2], ignore_index=True)
# 删除第一行
df.drop(1)
# 条件删除
df.drop(df[df.金牌数<20].index)
# 提取倒数后三列的10-20行
df.iloc[10:20,-3:]
df.loc[10:20, '总分':] 
# 提取第 10 行 
# DataFrame格式
a = df.loc[9:9]
# Series格式
a = df.loc[9,:]
# 提取第 10 行之后的全部行
df.iloc[9:,]
df.iloc[9:]
df.loc[9:]
# 提取 0-50 行，间隔为 3
df[:50:3]
# 提取 金牌数 不等于 10 的行
df.loc[~(df['金牌数'] == 10)]
# 提取奇数行
df[[i%2==1 for i in range(len(df.index))]]
# 提取 中国、美国、英国、日本、巴西 五行数据 且 金牌数小于30
df.loc[(df['金牌数'] < 30) & (df['国家奥委会'].isin(['中国','美国','英国','日本','巴西']))]
# 包含某个字的行
df[df.国家奥委会.str.contains('国')]
# 提取 第 0-2 行第 0-2 列
df.iloc[0:2,0:2]
df.iloc[0:2,[0,1]]
# 使用 query 提取 金牌数 + 银牌数 大于 15 的国家
df.query('金牌数+银牌数 > 15')
# 使用 query 提取 金牌数 大于 金牌均值的国家
gold_mean = df['金牌数'].mean()
df.query(f'金牌数 > {gold_mean}')
# 指定位置插入行
df1 = df.iloc[:1, :]
df2 = df.iloc[1:, :]
df3 = pd.DataFrame([[i for i in range(len(df.columns))]], columns=df.columns)
df_new = pd.concat([df1, df3, df2], ignore_index=True)
# 调整 顺序
q4_df = q4_df.reindex([0, 1, 2, 3, 4, 5, 6, 7, 8, 22, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]).reset_index()

pivot与groupby

1
2
3
4
5
pd.pivot_table(df2,values = ['奖牌类型'],index = ['国家','运动类别'],aggfunc = 'count')
# 等价于
pd.DataFrame(df2.groupby(['国家','运动类别']).count()['奖牌类型'])
# 等价于
df2.groupby(['国家','运动类别']).count()[['奖牌类型']]

unstack

1
2
3
4
5
6
# 计算前十名各国每日奖牌数量合计
# 注意：对于第一天没有数据的国家用0填充，其余时间的缺失值用上一日数据填充
countries = df2.groupby('国家').count().sort_values('奖牌类型',ascending=False).head(10).index.tolist()
tmp = df2[df2['国家'].isin(countries)]
tmp.groupby(['获奖时间','国家']).count()['奖牌类型'].unstack().cumsum().fillna(0)

数据聚合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
# 分组，但不作为索引
df.groupby("district", as_index=False)['salary'].mean()
# 分组统计
df.groupby("district")['companySize'].value_counts()
# 或者groupby两个
df.groupby(['district','companySize'])['companySize'].count()
# 查看group的结果
df.groupby(["district",'salary']).groups
# 将数据按照 district、salary 进行分组，并查看西湖区薪资为 30000 的工作
df.groupby(["district",'salary']).get_group(("西湖区",30000))
# 计算不同行政区(district)，不同规模公司(companySize)出现的次数
pd.DataFrame(df.groupby("district")['companySize'].value_counts()) #使用value_counts的方式，有时候比两个groupby好用
df.groupby(['district','companySize']).count().iloc[:,0:1]
# 分组
df['salary'].groupby([df['workYear'], df['education']]).mean()
df.groupby(['workYear', 'education']).mean()['salary']
# 在原数据框 df 新增一列，数值为该区的平均薪资水平
df['该区平均工资'] = df[['district','salary']].groupby(by='district').transform('mean')
# 通过匿名函数分组 根据 createTime 列，计算每天不同 行政区 新增的岗位数量
pd.DataFrame(df.groupby([df.createTime.apply(lambda x:x.day)])[
             'district'].value_counts()).rename_axis(["发布日", "行政区"])
# 计算各行政区的企业领域（industryField）包含电商的总数
df.groupby('district')["industryField"].apply(lambda x: x.str.contains('电商').sum())
# 计算各行政区的企业领域（industryField）包含电商的总数
df.groupby("district", sort=False)["industryField"].apply(
lambda x: x.str.contains("电商").sum())
#通过 positionName 的长度进行分组，并计算不同长度岗位名称的薪资均值
df.set_index("positionName").groupby(len)['salary'].mean()
df.groupby(df.positionName.apply(lambda x:len(x)))['salary'].mean()
# groupby 直接改名
df.groupby({'salary':'薪资','score':'总分','matchScore':'总分'}, axis=1).sum()
# groupby 用字典
#将 score 和 matchScore 的和记为总分，与 salary 列同时进行分组，并查看结果
df.groupby({'salary':'薪资','score':'总分','matchScore':'总分'}, axis=1).sum()
# 聚合
df['salary'].groupby(df['district']).mean() 
# 等价
df[['district','salary']].groupby('district').mean()
# 在原数据框 df 新增一列，数值为该区的平均薪资水平
df['该区平均工资'] = df[['district','salary']].groupby(by='district').transform('mean')
# 提取平均工资小于 30000 的行政区的全部数据
df.groupby('district').filter(lambda x: x['salary'].mean() < 30000)
# 分组计算不同行政区，薪水的最小值、最大值和平均值
df.groupby('district')['salary'].agg([min, max, np.mean])
# 对不同行政区进行分组，并统计薪水的均值、中位数、方差，以及得分的均值
df.groupby('district').agg(
    {'salary': [np.mean, np.median, np.std], 'score': np.mean})
# 通过 df2 计算获得奖牌最多的运动员
df2['运动员'].value_counts().sort_values(ascending=False).head(1)
# 查看各国在不同项目上的获奖牌情况
df2['总奖牌数'].groupby([df2['国家'],df2['运动类别']]).count().to_frame()
df2.groupby(['国家','运动类别']).count()['总奖牌数'].to_frame()
pd.pivot_table(df2,values = ['奖牌类型'],index = ['国家','运动类别'],aggfunc = 'count')
# 按照行计算平均值
df.mean(axis='columns')
df.mean(axis=1) #不是0，1是算每列的均值然后然后合并为一行
# 提取平均工资小于 30000 的行政区的全部数据
df.groupby('district').filter(lambda x: x['salary'].mean() < 30000)
# 聚合统计
import numpy as np
df.groupby('district')['salary'].agg([min, max, np.mean])
#查看缺失值比例，并排序  不是count！！！
data = df.isna().sum()/df.shape[0]
data.sort_values().map(lambda x:"{:.2%}".format(x))
#对不同岗位(positionName)进行分组，并统计其薪水(salary)中位数和得分(score)均值
df.groupby('positionName').agg({'salary': np.median, 'score': np.mean})
# 自定义函数
def myfunc(x):

    return x.max()-x.mean()

df.groupby('district').agg(最低工资=('salary', 'min'), 最高工资=(
    'salary', 'max'), 平均工资=('salary', 'mean'), 最大值与均值差值=('salary', myfunc)).rename_axis(["行政区"])

数据查询

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 查询某列的值为x时，即使该列为坐标
#查询中国队的获奖牌
df3.query("国家 == ['中国']")

#计算中国每日总奖牌数量 累计
df2.groupby(['获奖时间','国家']).count()['奖牌类型'].to_frame().query('国家==["中国"]').cumsum()


#查询空值所在行
df[df.isnull().T.any() == True]

# 查看重复的
df[df.duplicated()]

#查询条件
df_01.loc[df_01['行业（按行业大类）'].isin(['工业','建筑业'])]
df_01.loc[(df_01['行业（按行业大类）']=='工业')|(df_01['行业（按行业大类）']=='建筑业')]
df_01[df_01['行业（按行业大类）'].str.contains('工业|建筑业')]

数据汇总

1
2
3
4
5
# 计算 总分、高端人才得分、办学层次得分的最大最小值、中位数、均值
df.agg({
        "总分": ["min", "max", "median", "mean"],
        "高端人才得分": ["min", "max", "median", "mean"],
        "办学层次得分":["min", "max", "median", "mean"]})

数据合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 垂直拼接 df1、df2、df3，效果如下图所示
pd.concat([df1, df2, df3])
# 垂直拼接 df1 和 df4，并按顺序重新生成索引，
df = pd.concat([df1,df4]).reset_index()
# 或者
df = pd.concat([df1, df4], ignore_index=True)

# 横向拼接
pd.concat([df1,df4],axis=1)
# 在上一题的基础上，只取结果的交集
pd.concat([df1,df4],axis=1,join='inner')
# 只取包含 df1 索引的部分
pd.concat([df1, df4], axis=1).reindex(df1.index)
# 拼接 df1、df2、df3，同时新增一个索引（x、y、z）来区分不同的表数据来源
pd.concat([df1, df2, df3], keys=['x', 'y', 'z'])
# 根据 key 连接 left 和 right
pd.merge(left, right, on='key')
# 根据 key1 和 key2 连接 left 和 right
pd.merge(left, right, on=['key1', 'key2'])
'''
how 可以设置
	right、left: 左外，右外
	outer、inner: 全外连接，内连接
	
'''
pd.merge(left, right, how='left', on=['key1', 'key2'])
# 重新产生数据
left.join(right, on=['key1', 'key2'])

多个DF画一起

1
2
3
4
5
6
7
8
9
10
fig, ax = plt.subplots(figsize=(16,10))   
def to_percent(temp, position):
    return '%1.0f'%(100*temp) + '%'
plt.gca().yaxis.set_major_formatter(FuncFormatter(to_percent))
ax.plot(max_data,label='first one')
ax.plot(min_data,label='last one')
ax.plot(q3_df,label='mean')
ax.set_title('Daily Empty Rate Comparison For Village Y')
plt.legend(loc='best')
plt.savefig('C-4.png')

分析和排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 将空置率从低到高排序
q1_df=q1_df.sort_values('AT_HOME')
# 参数by可以忽略
df.sort_values(by='总分', ascending=True).head(20)
# 查看各项得分最高的学校名称
df.iloc[:,3:].idxmax()
# 统计 总分 列的均值
df['总分'].mean()
df.总分.mean()
# 计算总分列的中位数
df.总分.median()
# 计算总分列的众数
df.总分.mode()
# 查看数值型数据的统计信息（均值、分位数等），并保留两位小数
df.describe().round(2).T

双纵坐标轴

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 导入data.csv
df = pd.read_csv('data.csv')
# 将Date转为日期格式
df['Date'] = pd.to_datetime(df['Date'])
# 优化df的结构
df=df.reset_index(drop=True).set_index('Date')
# 选择数据范围 2014年1月1日至2018年7月31日
q1_df = df['2014-01-01':'2018-07-31']
# 构建画图使用的dataframe 每天的日电量、最高温度、最低温度
q1_plot_df = q1_df[['DailyElectricity','MaxTemperature','MinTemperature']]
# 画图
fig,ax = plt.subplots(figsize=(10,8))
ax.plot(df['DailyElectricity'],color='r',label='DailyElectricity')
# 镜像x轴
ax2 = ax.twinx()
ax2.plot(df['MaxTemperature'],color='b',label='MaxTemperature')
ax2.plot(df['MinTemperature'],color='g',label='MinTemperature')
# 添加图例
ax.legend(loc='best')
ax2.legend(loc='best')
ax.set_title('Daily Usage and Temperature')
plt.savefig('F-1.png')


构建空DF

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
max_data = pd.DataFrame(columns={'DATA_DATE','empty_ratio'})
min_data = pd.DataFrame(columns={'DATA_DATE','empty_ratio'})


for i in range(len(q4_df)):
    indx = q4_df.index[i][1]
    
    val = q4_df.iloc[i][0]
    if indx == 'Street A':
        max_data = max_data.append([{'DATA_DATE':q4_df.index[i][0],'empty_ratio':val}],ignore_index=True)
    if indx == 'Street G':
        min_data = min_data.append({'DATA_DATE':q4_df.index[i][0],'empty_ratio':val},ignore_index=True)
        
max_data=max_data.reset_index(drop=True).set_index(max_data['DATA_DATE']).drop('DATA_DATE',1)
min_data=min_data.reset_index(drop=True).set_index(min_data['DATA_DATE']).drop('DATA_DATE',1)
# 新建df 方法一

cols_q3=['类别','本周电量','上周周电量','环比提升','农历同期周电量','同比提升']
q3_df = pd.DataFrame(columns=cols_q3)
q3_df.loc[0]=np.nan #先新建一列
q3_df.iloc[0,0] = '软件园一期' # 第一次要iloc
q3_df.loc[1] = '软件园二期'   # 后面可以用iloc来做
q3_df.loc[2] = '软件园三期'
q3_df.loc[3] = '医药制造'q3_df.iloc[0,1] = bz_factory.iloc[1,1].round(2)
q3_df.iloc[0,2] = sz_factory['上周周电量'][0].round(2)
q3_df.iloc[0,3] = (bz_factory.iloc[1,1]-sz_factory['上周周电量'][0])/sz_factory['上周周电量'][0]
q3_df.iloc[0,4] = nl_factory.iloc[1,1].round(2)
q3_df.iloc[0,5] = (bz_factory.iloc[1,1]-nl_factory.iloc[1,1])/nl_factory.iloc[1,1]
# 新建df 方法二直接concat
q1_df.loc[0]=np.nan
tmp_df.loc[0]=np.nan

q1_df.iloc[0,0] = '工业'
tmp_df.iloc[0,0] = '建筑业'

q1_df.iloc[0,1]=bz_gy['开工指数'].round(2)
tmp_df.iloc[0,1]=bz_jz['开工指数'].round(2)

q1_df = pd.concat([q1_df,tmp_df],axis=0)
q1_df.to_csv('Q2-1.csv',index=False)

# 将一列添加到一个新的df里面，需要保证！！！index一致！！！ 否则加不进去
# q2_df
cols_q2 = ['类别','本周电量','上周周电量','环比提升','农历同期周电量','同比提升']
q2_df = pd.DataFrame(columns=cols_q2)
q2_df['类别']=usage_bz.T.index
q2_df['本周电量']=usage_bz.T.reset_index()['厦门市'] #要先reset_index
q2_df

更改日期间隔

1
2
# 更改日期间隔
plt.xticks(pd.date_range('2021-01-01','2021-03-31',freq='20D'))

查看统计数据

1
2
3
4
5
6
7
8
9
10
# 查看数据行列数
df.shape
# 查看数据量
df.size
# 查看 数值型 列的统计信息，计数、均值什么的
df.describe()
# 查看 离散型 列的统计信息，计数、频率什么
df.describe(include=['O'])
# 查看 全部 列的统计信息
df.describe(include='all')

保存文件

1
2
3
4
5
6
# 不保存索引
data.to_csv("out.csv",encoding = 'utf_8_sig',index = False)
# 保存指定列
data.to_csv("out.csv",encoding = 'utf_8_sig',columns=['positionName','salary'])
# 小数点
mar.to_csv("2-1.csv", index=False, float_format='%.3f')

数据预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# isnull() is an alias for isna 
# 计算缺失值
df.isna().sum().sum()
# 每列有多少缺失值
df.isnull().sum()
# 查看缺失值
df[df.isnull().T.any() == True]
# 将评价人数列的缺失值，用整列的均值进行填充
df['评价人数'] = df['评价人数'].fillna(df['评价人数'].mean())
# 现在将评分列的缺失值，替换为上一个电影的评分
df['评分'] = df['评分'].fillna(axis=0,method='ffill')
# 将评价人数列的缺失值，用上下数字的均值进行填充
df['评价人数'] = df['评价人数'].fillna(df['评价人数'].interpolate())
# 在填充 “语言” 列的缺失值，要求根据 “国家/地区” 列的值进行填充
df['语言']=df.groupby('国家/地区').语言.bfill()
# 查找重复值
df[df.duplicated()]
# 查找指定列的重复值
df[df.duplicated(['片名'])]
# 删除全部的重复值
df = df.drop_duplicates()
# 删除全部的重复值，但保留最后一次出现的值first/last/false
df = df.drop_duplicates(keep = 'last')
# 计算各省市出现的次数
df.省市.value_counts()



# 都可以用inplace=True来代替赋值

删除空行

1.函数详解

函数形式：dropna(axis=0, how=’any’, thresh=None, subset=None, inplace=False)

参数：

axis：轴。0或’index’，表示按行删除；1或’columns’，表示按列删除。

how：筛选方式。‘any’，表示该行/列只要有一个以上的空值，就删除该行/列；‘all’，表示该行/列全部都为空值，就删除该行/列。

thresh：非空元素最低数量。int型，默认为None。如果该行/列中，非空元素数量小于这个值，就删除该行/列。

subset：子集。列表，元素为行或者列的索引。如果axis=0或者‘index’，subset中元素为列的索引；如果axis=1或者‘column’，subset中元素为行的索引。由subset限制的子区域，是判断是否删除该行/列的条件判断区域。

inplace：是否原地替换。布尔值，默认为False。如果为True，则在原DataFrame上进行操作，返回值为None。

1
2
3
4
# 删除整行缺失的数据，剩余缺失数据按0值进行填充
df2 = df2.dropna(how='all').fillna(0)
# 删除某列为空的行
df_initial.dropna(axis = 0, subset = ['客户ID'], inplace = True)

替换

1
2
3
4
5
6
# 将金牌数列的数字 0 替换为 无
df['金牌数'].replace(0,'无',inplace=True)
#同时替换 1将 无 替换为 缺失值 2将 0 替换为 None
df.replace(['无',0],[np.nan,'None'],inplace = True)
# 将 `金牌数` 列类型修改为 `int`
df['金牌数'] = df['金牌数'].fillna('0').astype(int)

算法总结

分类 回归
分类树tree.DecisionTreeClassififier 回归树tree.DecisionTreeRegressor
随机森林ensemble.RandomForestClassifier 回归森林ensemble.RandomForestRegressor
逻辑回归linear_model.LogisticRegression
KNN neighbors .KNeighborsClassifier
Naive Bayes
梯度提升树木ensemble.GradientBoostingRegressor

决策树

决策树优点

  1. 易于理解和解释，因为树木可以画出来被看见

  2. 需要很少的数据准备。其他很多算法通常都需要数据规范化，需要创建虚拟变量并删除空值等。但请注意，sklearn中的决策树模块不支持对缺失值的处理。

  3. 使用树的成本（比如说，在预测数据的时候）是用于训练树的数据点的数量的对数，相比于其他算法，这是一个很低的成本。

  4. 能够同时处理数字和分类数据，既可以做回归又可以做分类。其他技术通常专门用于分析仅具有一种变量类型的数据集。

  5. 能够处理多输出问题，即含有多个标签的问题，注意与一个标签中含有多种标签分类的问题区别开

  6. 是一个白盒模型，结果很容易能够被解释。如果在模型中可以观察到给定的情况，则可以通过布尔逻辑轻松解释条件。相反，在黑盒模型中（例如，在人工神经网络中），结果可能更难以解释。

  7. 可以使用统计测试验证模型，这让我们可以考虑模型的可靠性。

  8. 即使其假设在某种程度上违反了生成数据的真实模型，也能够表现良好。

决策树的缺点

  1. 决策树学习者可能创建过于复杂的树，这些树不能很好地推广数据。这称为过度拟合。修剪，设置叶节点所需的最小样本数或设置树的最大深度等机制是避免此问题所必需的，而这些参数的整合和调整对初学者来说会比较晦涩

  2. 决策树可能不稳定，数据中微小的变化可能导致生成完全不同的树，这个问题需要通过集成算法来解决。

  3. 决策树的学习是基于贪婪算法，它靠优化局部最优（每个节点的最优）来试图达到整体的最优，但这种做法不能保证返回全局最优决策树。这个问题也可以由集成算法来解决，在随机森林中，特征和样本会在分枝过程中被随机采样。

  4. 有些概念很难学习，因为决策树不容易表达它们，例如XOR，奇偶校验或多路复用器问题。

  5. 如果标签中的某些类占主导地位，决策树学习者会创建偏向主导类的树。因此，建议在拟合决策树之前平衡数据集。