面试常考的coding
牛客网输入输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
import java.util.*;
public class Next {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int N=sc.nextInt();
int[] num = new int[N];
for (int i = 0; i < N; i++) {
num[i] = sc.nextInt();
}
}
}
import java.util.*;
public class Main{
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.nextLine();
char[] arr = str.toCharArray();
}
}
public class Demo1 {
private int N;
private String[] arr;
private int count;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
arr = new String[demo.N];
for (int i = 0; i < demo.N; i++) {
String str = sc.next();
}
sc.close();
}
|
树
树的前序遍历 -
1
2
3
4
5
6
7
8
9
10
11
12
13
| public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList();
if(root==null) return res;
Stack<TreeNode> s = new Stack();
s.push(root);
while(!s.isEmpty()){
root=s.pop();
res.add(root.val);
if(root.right!=null) s.push(root.right);
if(root.left!=null) s.push(root.left);
}
return res;
}
|
树的中序遍历 -
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList();
if(root==null) return res;
Stack<TreeNode> s = new Stack();
while(!s.isEmpty()||root!=null){
if(root!=null){
while(root!=null){
s.push(root);
root=root.left;
}
}else{
root = s.pop();
res.add(root.val);
root=root.right;
}
}
return res;
}
|
树的后序遍历 -
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList();
if(root==null) return res;
Stack<TreeNode> s1 = new Stack();
Stack<TreeNode> s2 = new Stack();
s1.push(root);
while(!s1.isEmpty()){
TreeNode tmp = s1.pop();
s2.push(tmp);
if(tmp.left!=null) s1.push(tmp.left);
if(tmp.right!=null) s1.push(tmp.right);
}
while(!s2.isEmpty()) res.add(s2.pop().val);
return res;
}
|
设计模式
工厂模式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| public interface FoodFactroy{
Food makeFood(String name);
}
public class ChineseFoodFactory implements FoodFactory{
public Food makeFood(String name){
if(name.equals("A")){
return new ChineseFoodA();
}else if (name.equals("B")) {
return new ChineseFoodB();
} else {
return null;
}
}
}
public class AmericanFoodFactory implements FoodFactory {
@Override
public Food makeFood(String name) {
if (name.equals("A")) {
return new AmericanFoodA();
} else if (name.equals("B")) {
return new AmericanFoodB();
} else {
return null;
}
}
}
public class APP {
public static void main(String[] args) {
FoodFactory factory = new ChineseFoodFactory();
Food food = factory.makeFood("A");
}
}
|
单例模式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public class Singleton{
private static volatile Singleton instance=null;
private Singleton(){}
public Singleton(){
if(instance==null){
synchronized(Singleton.class){
if(instance==null){
instance = new Singleton();
}
}
}
return instance;
}
}
|
第一个 if 语句用来避免 uniqueInstance 已经被实例化之后的加锁操作,而第二个 if 语句进行了加锁,所以只能有一个线程进入,就不会出现 uniqueInstance == null 时两个线程同时进行实例化操作。
的, uniqueInstance = new Singleton(); 这段代码其实是分为三步执行:
- 为 uniqueInstance 分配内存空间
- 初始化 uniqueInstance
- 将 uniqueInstance 指向分配的内存地址
使用 volatile 可以禁止 JVM 的指令重排,保证在多线程环境下也能正常运行。
算法
死锁
1
2
3
4
5
6
7
8
9
| public class DeadLock {
static final Object lock1=new Object();
static final Object lock2=new Object();
public static void main(String[] args) {
new Thread(new A()).start();
new Thread(new B()).start();
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class A implements Runnable {
@Override
public void run() {
while(true){
synchronized(DeadLock.lock1){
System.out.println("A get lock1");
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
synchronized (DeadLock.lock2){
System.out.println("A get lock2");
}
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public class B implements Runnable {
public void run() {
while(true){
synchronized(DeadLock.lock2){
System.out.println("B get lock2");
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
synchronized (DeadLock.lock1){
System.out.println("B get lock1");
}
}
}
}
}
|
一.什么是死锁?
死锁是由于两个或以上的线程互相持有对方需要的资源,导致这些线程处于等待状态,无法执行。
二.产生死锁的四个必要条件
1.互斥性:线程对资源的占有是排他性的,一个资源只能被一个线程占有,直到释放。
2.请求和保持条件:一个线程对请求被占有资源发生阻塞时,对已经获得的资源不释放。
3.不剥夺:一个线程在释放资源之前,其他的线程无法剥夺占用。
4.循环等待:发生死锁时,线程进入死循环,永久阻塞。
三.避免死锁的方法
1.破坏“请求和保持”条件
一次性申请所有需要用到的资源,不要一次一次来申请,当申请的资源有一些没空,那就让线程等待。不过这个方法比较浪费资源,进程可能经常处于饥饿状态。还有一种方法是,要求进程在申请资源前,要释放自己拥有的资源。
2.破坏“不可抢占”条件
允许进程进行抢占,方法一:如果去抢资源,被拒绝,就释放自己的资源。方法二:操作系统允许抢,只要你优先级大,可以抢到。
3.破坏“循环等待”条件
将系统中的所有资源统一编号,进程可在任何时刻提出资源申请,但所有申请必须按照资源的编号顺序(升序)提出
LRU
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| class LRUCache {
int cap,count;
HashMap<Integer,Node> map=new HashMap();
Node head,tail;
class Node{
Node pre,next;
int val,key;
public Node(int key,int value){
this.key=key;
this.val=value;
}
public Node(){
this(0,0);
}
}
public LRUCache(int capacity) {
cap=capacity;
count=0;
head=new Node();
tail=new Node();
head.next=tail;
tail.pre=head;
}
public int get(int key) {
Node n = map.get(key);
if(n==null) return -1;
remove(n);
add(n);
return n.val;
}
public void put(int key, int value) {
Node n = map.get(key);
if(n==null){
n = new Node(key,value);
map.put(key,n);
add(n);
count++;
}else{
n.val=value;
remove(n);
add(n);
}if(count>cap){
Node del=tail.pre;
remove(del);
map.remove(del.key);
count--;
}
}
public void add(Node n){
Node after=head.next;
head.next=n;
n.pre=head;
n.next=after;
after.pre=n;
}
public void remove(Node n){
Node before=n.pre,after=n.next;
before.next=after;
after.pre=before;
}
}
|
生产者消费者
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| public class ClothesFactory{
private final int size=10;
private LinkedList<Object> list = new LinkedList();
public void produce(){
synchronized(list){
while(list.size()>=size){
try{
list.wait();
}catch(InterruptedException e){
e.printStackTrace();
}
}
list.addFirst(new Object());
list.notifyAll();
}
}
public void comsume(){
synchronized(list){
while(list.size()<=0){
try{
list.wait();
}catch(InterruptedException e){
e.printStackTrace();
}
}
list.removeLast();
list.notifyAll();
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class Producer implements Runnable{
private ClothesFactory clothesFactory;
public Producer(ClothesFactory clothesFactory){
this.clothesFactory=clothesFactory;
}
public void run(){
while(true){
try{
clothesFactory.produce();
}catch(InterruptedException e){
e.printStackTrace();
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public class Comsumer implements Runnable{
private ClothesFactory clothesFactory;
public Comsumer(ClothesFactory clothesFactory){
this.clothesFactory=clothesFactory;
}
public void run(){
while(true){
try{
clothesFactory.comsume();
}catch(InterruptedException e){
e.printStackTrace();
}
}
}
}
|
排序
分析时间复杂度
快排 √
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public void sort(int a[]){
int lo=0,hi=a.length-1;
if(lo<hi){
int mid = qs(a,lo,hi);
sort(a,lo,mid-1);
sort(a,mid+1,hi);
}
}
public void qs(int[] a,int lo,int hi){
int i=lo,j=hi,x=a[lo];
if(i<j){
while(i<j&&a[j]>=x)j--;
if(i<j) a[i]=a[j];
while(i<j&&a[i]<x)i++;
if(i<j) a[j]=a[i];
}
a[i]=x;
return i;
}
|
1、最优情况
在最优情况下,Partition每次都划分得很均匀,如果排序n个关键字,其递归树的深度就为 [log2n]+1( [x] 表示不大于 x 的最大整数),即仅需递归 log2n 次,需要时间为T(n)的话,第一次Partiation应该是需要对整个数组扫描一遍,做n次比较。然后,获得的枢轴将数组一分为二,那么各自还需要T(n/2)的时间(注意是最好情况,所以平分两半)。于是不断地划分下去,就有了下面的不等式推断:

2、最糟糕情况
然后再来看最糟糕情况下的快排,当待排序的序列为正序或逆序排列时,且每次划分只得到一个比上一次划分少一个记录的子序列,注意另一个为空。如果递归树画出来,它就是一棵斜树。此时需要执行n‐1次递归调用,且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录,也就是枢轴的位置,因此比较次数为
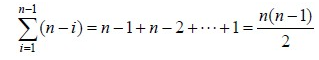
快速选择 √
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public void select(int a[],int k){
int lo=0,hi=a.length-1;
k--;
if(lo<hi){
int mid = qs(a,lo,hi);
if(mid>k){
hi=mid-1;
}else if(mid==k){
break;
}else{
lo=mid+1;
}
}
}
public void qs(int[] a,int lo,int hi){
int i=lo,j=hi,x=a[lo];
if(i<j){
while(i<j&&a[j]>=x)j--;
if(i<j) a[i]=a[j];
while(i<j&&a[i]<x)i++;
if(i<j) a[j]=a[i];
}
a[i]=x;
return i;
}
|
堆排
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public void heap(int[] a){
int len = a.length;
build(a,len);
for(int i=len-1;i>0;i--){
int tmp=a[0];
a[0]=a[i];
a[i]=tmp;
len--;
sink(a,0,len);
}
}
public void build(int[] a,int len){
for(int i=len/2;i>=0;i--){
sink(a,i,len);
}
}
public void sink(int[] a,int i,int len){
int left=i*2+1;
int right=2*i+2;
int present=i;
if(left<len&&a[left]>a[present]) present=left;
if(right<len&&a[right]>a[present]) present=right;
if(present!=i){
int tmp=a[i];
a[i]=a[present];
a[present]=tmp;
sink(a,present,len);
}
}
|
在构建堆的过程中,因为我们是完全二叉树从最下层最右边的非终端结点开始构建,将它与其孩子进行比较和若有必要的互换,对于每个非终端结点来说,其实最多进行两次比较和互换操作,因此整个构建堆的时间复杂度为O(n)。
在正式排序时,第i次取堆顶记录重建堆需要用O(logi)的时间(完全二叉树的某个结点到根结点的距离为.log2i.+1),并且需要取n-1次堆顶记录,因此,重建堆的时间复杂度为O(nlogn)。
归并排序 √
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public void merge(int a[]){
return sort(a,0,a.length-1,new int[a.length]);
}
public void sort(int[] a,int lo,int hi,int[] tmp){
int lo=0,hi=a.length-1;
if(lo<hi){
int mid = lo+(hi-lo)/2;
sort(a,lo,mid,tmp);
sort(a,mid+1,hi,tmp);
mergeArray(a,lo,mid,hi,tmp);
}
}
public void mergeArray(int[] a,int lo,int mid,int hi,int[] tmp){
int i=lo,m=mid,j=mid+1,n=hi,k=0;
while(i<=m&&j<=n){
if(a[i]<=a[j]){
tmp[k++]=a[i++];
}else{
tmp[k++]=a[j++];
}
}
while(i<=m) tmp[k++]=a[i++];
while(j<=n) tmp[k++]=a[j++];
for(int l=0;l<=k;l++){
a[l+lo]=tmp[l];
}
}
|
公式:T[n] = 2T[n/2] + O(n);