树

摘录了一些经典的树的题，一共题。

• 树的重建
  • 105. Construct Binary Tree from Preorder and Inorder Traversal -
  • 106. Construct Binary Tree from Inorder and Postorder Traversal -
  • 297. Serialize and Deserialize Binary Tree -
  • 109. Convert Sorted List to Binary Search Tree -
  • 99. Recover Binary Search Tree ×
• 树的遍历（回溯）
  • 94. Binary Tree Inorder Traversal (Iteratively) ×
  • 144. Binary Tree Preorder Traversal (Iteratively) ×
  • 145. Binary Tree Postorder Traversal (Iteratively) ×
  • 103. Binary Tree Zigzag Level Order Traversal √
  • 102. Binary Tree Level Order Traversal √
  • 107. Binary Tree Level Order Traversal II √
  • 637. Average of Levels in Binary Tree √
  • 515. Find Largest Value in Each Tree Row √
  • 513. Find Bottom Left Tree Value √
  • 1302. Deepest Leaves Sum √
  • 226. Invert Binary Tree √
  • 112. Path Sum √
  • 111. Minimum Depth of Binary Tree √
  • 437. Path Sum III -
  • 404. Sum of Left Leaves ×
  • 687. Longest Univalue Path ×
  • 337. House Robber III √
  • 590. N-ary Tree Postorder Traversal √
  • 589. N-ary Tree Preorder Traversal √
  • 559. Maximum Depth of N-ary Tree √
  • 337. House Robber III -
• 树的性质
  • 897. Increasing Order Search Tree ×
  • 671. Second Minimum Node In a Binary Tree ×
  • 98. Validate Binary Search Tree -
  • 110. Balanced Binary Tree √
• 两棵树的判断
  • 101. Symmetric Tree √
  • 100. Same Tree √
  • 617. Merge Two Binary Trees √
  • 572. Subtree of Another Tree √

树的重建

105. Construct Binary Tree from Preorder and Inorder Traversal -

Given preorder and inorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]

Return the following binary tree:

  3
 / \
9  20
  /  \
 15   7

public TreeNode buildTree(int[] preorder, int[] inorder) {
    return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
}

private TreeNode build(int[] preorder, int preS, int preE, int[] inorder, int inS, int inE) {
    if(preE>preS||inE>inS) return null;
    TreeNode root=new TreeNode(preorder[preS]);
    for (int i = inS; i <=inE; i++) {
        if(inorder[i]==preorder[preS]){
            root.left=build(preorder,preS+1,preS+i-inS,inorder,inS,i-1);
            root.right=build(preorder,preS+i-inS+1,preE,inorder,i+1,inE);
        }
    }
    return root;
}

对inorder来说i就是找到的位置，但是对post或者pre来说必须和i-inS有关

106. Construct Binary Tree from Inorder and Postorder Traversal -

Given inorder and postorder traversal of a tree, construct the binary tree.

Note:
You may assume that duplicates do not exist in the tree.

For example, given

inorder = [9,3,15,20,7]
postorder = [9,15,7,20,3]

Return the following binary tree:

  3
 / \
9  20
  /  \
 15   7

public TreeNode buildTree(int[] inorder, int[] postorder) {
    return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
}

private TreeNode build(int[] inorder, int inS, int inE, int[] postorder, int poS, int poE) {
    if(inS>inE||poS>poE) return null;
    TreeNode root = new TreeNode(postorder[poE]);
    for (int i = inS; i <=inE ; i++) {
        if(inorder[i]==postorder[poE]){
            root.left=build(inorder,inS,i-1,postorder, poS, poS+i-inS-1);
            root.right=build(inorder,i+1,inE,postorder,poS+i-inS,poE-1);
        }
    }
    return root;
}

297. Serialize and Deserialize Binary Tree -

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Example:

You may serialize the following tree:

    1
   / \
  2   3
     / \
    4   5

as "[1,2,3,null,null,4,5]"

• 递归版本：

  public String serialize(TreeNode root) {
         StringBuilder sb = new StringBuilder();
         buildString(root, sb);
         return sb.toString();
     }
  
     private void buildString(TreeNode node, StringBuilder sb) {
         if (node == null) {
             sb.append("#,");
         } else {
             sb.append(node.val+",");
             buildString(node.left, sb);
             buildString(node.right,sb);
         }
     }
     // Decodes your encoded data to tree.
     public TreeNode deserialize(String data) {
         Deque<String> nodes = new LinkedList<>();
         nodes.addAll(Arrays.asList(data.split(",")));
         return buildTree(nodes);
     }
  
     private TreeNode buildTree(Deque<String> nodes) {
         String val = nodes.remove();
         if (val.equals("#")) return null;
         else {
             TreeNode node = new TreeNode(Integer.valueOf(val));
             node.left = buildTree(nodes);
             node.right = buildTree(nodes);
             return node;
         }
     }

• 迭代版本：

  public String serialize(TreeNode root) {
         if(root==null) return "";
         StringBuilder sb = new StringBuilder();
         Queue<TreeNode> q = new LinkedList();
         q.offer(root);
         while(!q.isEmpty()){
            TreeNode tmp = q.poll();
                 if(tmp==null){
                     sb.append("#,");
                     continue;
                 }
                 sb.append(tmp.val+",");
                 q.offer(tmp.left);
                 q.offer(tmp.right); 
                 
             
         }
         return sb.toString();
     }
    
     // Decodes your encoded data to tree.
     public TreeNode deserialize(String data) {
         if(data.length()==0) return null;
         String str[]=data.split(",");
         TreeNode root=new TreeNode(Integer.valueOf(str[0]));
         Queue<TreeNode> q= new LinkedList();
         q.offer(root);
         for(int i=1;i<str.length;i++){
             TreeNode parent = q.poll();
             if(!str[i].equals("#")){
                 TreeNode left=new TreeNode(Integer.valueOf(str[i]));
                 parent.left=left;
                 q.offer(left);
             }
             if(!str[++i].equals("#")){
                 TreeNode right=new TreeNode(Integer.valueOf(str[i]));
                 parent.right=right;
                 q.offer(right);
             }
         }
         return root;
         
     }

109. Convert Sorted List to Binary Search Tree -

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

• 暴力法：

public TreeNode sortedListToBST(ListNode head) {
       if(head==null) return null;
       int len = find(head);
       return build(head,0,len-1);
   }
   public TreeNode build(ListNode head,int lo,int hi){
       if(hi<lo) return null;        
       int mid = lo + (hi-lo)/2;
       TreeNode root = new TreeNode(getVal(head,mid));
       root.left=build(head,lo,mid-1);
       root.right=build(head,mid+1,hi);
       return root;
   }
   public int getVal(ListNode head, int index){
       int i=0;
       while(i<index){
           head=head.next;
           i++;
       }
       return head.val;
   }
   public int find(ListNode head){
       int i=0;
       while(head!=null){
           i+=1;
           head=head.next;
       }
       return i;
   }

• 正解

public TreeNode sortedListToBST(ListNode head) {
    if(head==null) return null;
    return toBST(head,null);
}
public TreeNode toBST(ListNode head, ListNode tail){
    ListNode slow = head;
    ListNode fast = head;
    if(head==tail) return null;

    while(fast!=tail&&fast.next!=tail){
        fast = fast.next.next;
        slow = slow.next;
    }
    TreeNode thead = new TreeNode(slow.val);
    thead.left = toBST(head,slow);
    thead.right = toBST(slow.next,tail);
    return thead;
}

99. Recover Binary Search Tree ×

Two elements of a binary search tree (BST) are swapped by mistake.

Recover the tree without changing its structure.

Example 1:

Input: [1,3,null,null,2]

   1
  /
 3
  \
   2

Output: [3,1,null,null,2]

   3
  /
 1
  \
   2

Example 2:

Input: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

Output: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

public void recoverTree(TreeNode root) {
       int swap[] = new int[2];
       TreeNode[] tree =new TreeNode[2];
       int index=0;
       dfs(root,swap,index,tree);
       swap(swap,tree);
       System.out.println();
   }

   private void swap(int[] swap, TreeNode[] tree) {
       tree[0].val = swap[1];
       tree[1].val=swap[0];
   }

   public void dfs(TreeNode root, int[] swap,int index,TreeNode[] tree){
       if(root==null)
           return;
       if(root.left!=null){
           if(root.val<root.left.val){
               swap[index]=root.val;
               tree[index]=root;
               index++;
           }
           dfs(root.left,swap,index,tree);
       }
       if(root.right!=null) {
           if(root.val>root.right.val){
               swap[index]=root.val;
               tree[index]=root;
               index++;
           }
           dfs(root.left,swap,index,tree);
       }
   }

树的遍历（回溯）

94. Binary Tree Inorder Traversal (Iteratively) ×

Given a binary tree, return the inorder traversal of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,3,2]

public List<Integer> inorderTraversal(TreeNode root) {
       List<Integer> res = new ArrayList();
       Stack<TreeNode> s = new Stack();
       if(root==null) return res;       
       while(root!=null||!s.isEmpty()){
           if(root!=null){
               s.push(root);
               root=root.left;
           }else{
               root=s.pop();
               res.add(root.val);
               root=root.right;
           }
       }
       return res;
   }

144. Binary Tree Preorder Traversal (Iteratively) ×

Given a binary tree, return the preorder traversal of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,2,3]

public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList();
        Stack<TreeNode> s = new Stack();
        if(root==null) return res;
        s.push(root);
        while(!s.isEmpty()){
            TreeNode tmp = s.pop();
            res.add(tmp.val);
            if(tmp.right!=null) s.push(tmp.right);
            if(tmp.left!=null) s.push(tmp.left);
        }
        return res;
    }

145. Binary Tree Postorder Traversal (Iteratively) ×

Given a binary tree, return the postorder traversal of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [3,2,1]

public List<Integer> postorderTraversal(TreeNode head) {
        List<Integer> list=new ArrayList<Integer>();
       Stack<TreeNode> stack1=new Stack<TreeNode>();
       Stack<TreeNode> stack2=new Stack<TreeNode>();
       if (head==null) return list;
       stack1.push(head);
       while(!stack1.empty()) {
           head=stack1.pop();
           stack2.push(head);
           if (head.left!=null) {
               stack1.push(head.left);
           }
           if (head.right!=null) {
               stack1.push(head.right);
           }
       }
       while(!stack2.empty()) {
           list.add(stack2.pop().val);
       }
       return list;
   }

103. Binary Tree Zigzag Level Order Traversal √

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example:
Given binary tree [3,9,20,null,null,15,7],

  3
 / \
9  20
  /  \
 15   7

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
    if(root==null) return new ArrayList();
    List<List<Integer>> res = new ArrayList();
    LinkedList<TreeNode> q = new LinkedList();
    q.add(root);
    int order = 1;
    while(!q.isEmpty()){
        int len = q.size();
        List<Integer> tmp = new ArrayList();
        for(int i=len-1;i>=0;i--){
            TreeNode t =q.poll();
            if (order == -1) {
                tmp.add(0, t.val);
            } else {
                tmp.add(t.val);
            }

            if(t.left!=null) q.offer(t.left);
            if(t.right!=null) q.offer(t.right);
        }
        res.add(tmp);
        order=order*-1;
    }
    return res;
}

102. Binary Tree Level Order Traversal √

Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

For example:
Given binary tree [3,9,20,null,null,15,7],

  3
 / \
9  20
  /  \
 15   7

return its level order traversal as:

[
  [3],
  [9,20],
  [15,7]
]

public List<List<Integer>> levelOrder(TreeNode root) {
       if(root==null) return new ArrayList();
       List<List<Integer>> res = new ArrayList();
       Queue<TreeNode> q = new LinkedList();
       q.add(root);
       while(!q.isEmpty()){
           int len = q.size();
           List<Integer> tmp = new ArrayList();
           for(int i=0;i<len;i++){
               TreeNode t =q.poll();
               tmp.add(t.val);
               if(t.left!=null) q.offer(t.left);
               if(t.right!=null) q.offer(t.right);
           }
           res.add(tmp);
       }
        return res;
   }

107. Binary Tree Level Order Traversal II √

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example:
Given binary tree [3,9,20,null,null,15,7],

  3
 / \
9  20
  /  \
 15   7

return its bottom-up level order traversal as:

[
  [15,7],
  [9,20],
  [3]
]

public List<List<Integer>> levelOrderBottom(TreeNode root) {
       if(root==null) return new ArrayList();
       List<List<Integer>> ans = new ArrayList();       
       Queue<TreeNode> q = new LinkedList();
       q.add(root);
       while(!q.isEmpty()){
           int len = q.size();
           List<Integer> t = new ArrayList();
           for(int i=0;i<len;i++){
               TreeNode tmp = q.poll();
               int val = tmp.val;
               t.add(val);
               if(tmp.left!=null) q.offer(tmp.left);
               if(tmp.right!=null) q.offer(tmp.right);
           }
           ans.add(0,new ArrayList(t));
       }
      
       return ans;
   }

637. Average of Levels in Binary Tree √

Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.

Example 1:

Input:
    3
   / \
  9  20
    /  \
   15   7
Output: [3, 14.5, 11]
Explanation:
The average value of nodes on level 0 is 3,  on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].

public List<Double> averageOfLevels(TreeNode root) {
    if(root==null) return null;
    Queue<TreeNode> q = new LinkedList();
    List<Double> res = new ArrayList();
    q.add(root);

    while(!q.isEmpty()){
        int len = q.size();
        double val=0.0;
        for(int i=0;i<len;i++){
            TreeNode tmp = q.poll();
            val+=tmp.val;
            if(tmp.left!=null) q.offer(tmp.left);
            if(tmp.right!=null) q.offer(tmp.right);
        }
        res.add(val/len);
    }
    return res;
}

515. Find Largest Value in Each Tree Row √

You need to find the largest value in each row of a binary tree.

Example:

Input: 

          1
         / \
        3   2
       / \   \  
      5   3   9 

Output: [1, 3, 9]

public List<Integer> largestValues(TreeNode root) {
    if(root==null) return new ArrayList();
    List<Integer> res = new ArrayList();
    Queue<TreeNode> q = new LinkedList();
    q.add(root);
    while(!q.isEmpty()){
        int tmp = Integer.MIN_VALUE;
        int len = q.size();
        for(int i=0;i<len;i++){
            TreeNode node = q.poll();
            tmp = node.val > tmp? node.val:tmp;
            if(node.left!=null) q.offer(node.left);
            if(node.right!=null) q.offer(node.right);
        }
        res.add(tmp);
    }
    return res;
}

513. Find Bottom Left Tree Value √

Given a binary tree, find the leftmost value in the last row of the tree.

Example 1:

Input:

    2
   / \
  1   3

Output:
1

Example 2:

Input:

        1
       / \
      2   3
     /   / \
    4   5   6
       /
      7

Output:
7

public int findBottomLeftValue(TreeNode root) {
    if (root == null) return 0;

    int result = 0;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);

    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (i == 0) result = node.val;
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
    }

    return result;
}

• 简化版：

public int findBottomLeftValue(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        root = queue.poll();
        if (root.right != null) queue.add(root.right);
        if (root.left != null) queue.add(root.left);
    }
    return root.val;
}

1302. Deepest Leaves Sum √

Given a binary tree, return the sum of values of its deepest leaves.

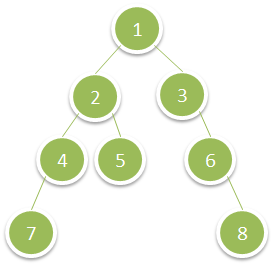
Example 1:

Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

public int deepestLeavesSum(TreeNode root) {
        if(root==null) return 0;
        int sum=0;
         ArrayList<Integer> rec = new ArrayList();
        Queue<TreeNode> q = new LinkedList();
        q.add(root);
        while(!q.isEmpty()){
            int len = q.size();
            rec.clear();
            for(int i=0;i<len;i++){
                TreeNode tmp = q.poll();
                rec.add(tmp.val);
                if(tmp.left!=null) q.offer(tmp.left);
                if(tmp.right!=null) q.offer(tmp.right);
            }
        }
        for(int i:rec) sum+=i;
        return sum;
    }

226. Invert Binary Tree √

Invert a binary tree.

Example:

Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

public TreeNode invertTree(TreeNode root) {
        if(root==null) return null;
        invert(root);
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
    public void invert(TreeNode root){
        if(root==null) return;
        TreeNode tmp = root.left;
        root.left=root.right;
        root.right=tmp;
    }

112. Path Sum √

public boolean hasPathSum(TreeNode root, int sum) {
        if(root==null) return false;
        if(sum==root.val&&root.left==root.right) return true;
       
        return hasPathSum(root.right,sum-root.val)|| hasPathSum(root.left,sum-root.val);
    }

111. Minimum Depth of Binary Tree √

public int minDepth(TreeNode root) {
       if(root==null) return 0;
       return find(root,1);
   }
   public int find(TreeNode root,int depth){
       if(root==null) return 0;
       if(root.left==root.right) return depth;
       int left=find(root.left,depth+1);
       int right=find(root.right,depth+1);
       return (left==0||right==0)?left+right:Math.min(left,right);
   }

437. Path Sum III -

You are given a binary tree in which each node contains an integer value.

Find the number of paths that sum to a given value.

The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).

The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.

Example:

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

public int pathSum(TreeNode root, int sum) {
       if (root == null) return 0;
       return pathSumFrom(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
   }
   
   private int pathSumFrom(TreeNode node, int sum) {
       if (node == null) return 0;
       return (node.val == sum ? 1 : 0) 
           + pathSumFrom(node.left, sum - node.val) + pathSumFrom(node.right, sum - node.val);
   }

404. Sum of Left Leaves ×

Find the sum of all left leaves in a given binary tree.

Example:

    3
   / \
  9  20
    /  \
   15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.

 public int sumOfLeftLeaves(TreeNode root) {
    if (root == null) return 0;
    if (isLeaf(root.left)) return root.left.val + sumOfLeftLeaves(root.right);
    return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}

private boolean isLeaf(TreeNode node){
    if (node == null) return false;
    return node.left == null && node.right == null;
}

687. Longest Univalue Path ×

Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.

The length of path between two nodes is represented by the number of edges between them.

Example 1:

Input:

    5
   / \
  4   5
 / \   \
1   1   5

Output: 2

Example 2:

Input:

    1
   / \
  4   5
 / \   \
4   4   5

Output: 2

public int longestUnivaluePath(TreeNode root) {
       if (root == null) return 0;
       int left = helper(root.left, root.val);
       int right = helper(root.right, root.val);
      return Math.max(left + right, Math.max(longestUnivaluePath(root.left), longestUnivaluePath(root.right)));
       
   }
   public int helper(TreeNode root, int val) {
       if (root == null || root.val != val) return 0;
       return 1 + Math.max(helper(root.left, val), helper(root.right, val));
   } 

337. House Robber III √

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Determine the maximum amount of money the thief can rob tonight without alerting the police.

Example 1:

Input: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

Output: 7 
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

Input: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

public int rob(TreeNode root) {
    if (root == null) return 0;
    
    int val = 0;
    
    if (root.left != null) {
        val += rob(root.left.left) + rob(root.left.right);
    }
    
    if (root.right != null) {
        val += rob(root.right.left) + rob(root.right.right);
    }
    
    return Math.max(val + root.val, rob(root.left) + rob(root.right));
}

直接用层次遍历就可以做。

590. N-ary Tree Postorder Traversal √

Given an n-ary tree, return the postorder traversal of its nodes’ values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Follow up:

Recursive solution is trivial, could you do it iteratively?

Example 1:

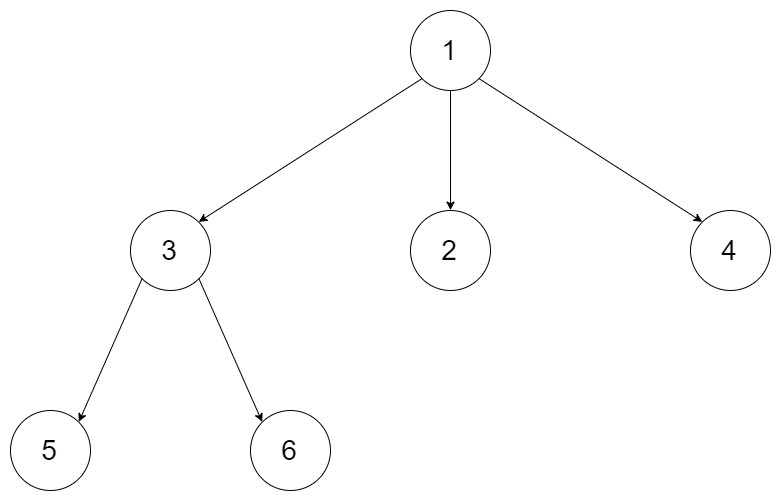
Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]

Example 2:

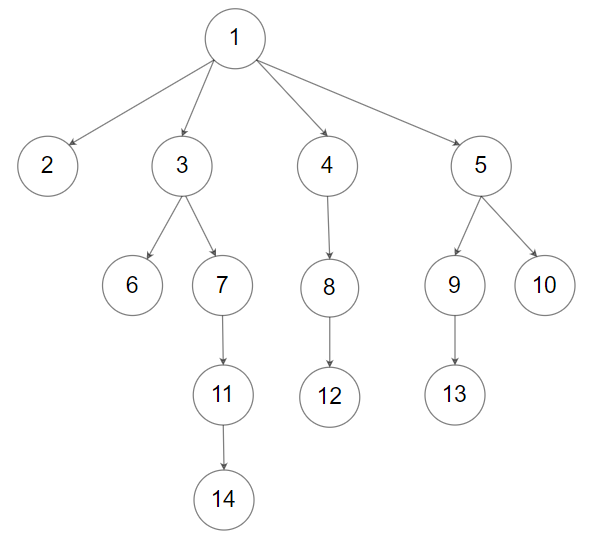
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [2,6,14,11,7,3,12,8,4,13,9,10,5,1]

public List<Integer> postorder(Node root) {
        List<Integer> res=new ArrayList();
       if(root==null) return res;      
       postT(root,res);
       res.add(root.val);
       return res;
   }
   public void postT(Node root, List<Integer> res){
        if(root==null) return;
        for(Node c: root.children){
           postT(c,res);
           res.add(c.val);
       }   
       
   }

589. N-ary Tree Preorder Traversal √

Given an n-ary tree, return the preorder traversal of its nodes’ values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Follow up:

Recursive solution is trivial, could you do it iteratively?

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: [1,3,5,6,2,4]

public List<Integer> preorder(Node root) {
       List<Integer> res =new ArrayList();
       if(root==null) return res;
       res.add(root.val);
       find(root,res);           
       return res;
   }
   public void find(Node root,List<Integer> res){
       if(root!=null) {
           for(Node n:root.children){
               res.add(n.val);
               find(n,res);
           }
       } 
   }

559. Maximum Depth of N-ary Tree √

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

public int maxDepth(Node root) {       
        return dfs(root, 1);
   }
   private int dfs(Node root, int depth) {
       int res=depth;
       if (root==null) return 0;         
       for (Node child:root.children) {
           res=Math.max(dfs(child, depth+1),res);
       }
       return res;
   }

337. House Robber III -

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Determine the maximum amount of money the thief can rob tonight without alerting the police.

Example 1:

Input: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \ 
     3   1

Output: 7 
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

Input: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \ 
 1   3   1

Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

public int rob(TreeNode root) {
       if(root==null) return 0;
       int v1 = root.val,v2=0;
       if(root.left!=null){
           v2+=rob(root.left);
           v1+=rob(root.left.right)+rob(root.left.left);
       }
       if(root.right!=null){
           v2+=rob(root.right);
           v1+=rob(root.right.right)+rob(root.right.left);
       }
       return Math.max(v1,v2);
   }

树的性质

897. Increasing Order Search Tree ×

Given a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only 1 right child.

Example 1:
Input: [5,3,6,2,4,null,8,1,null,null,null,7,9]

       5
      / \
    3    6
   / \    \
  2   4    8
 /        / \ 
1        7   9

Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

 1
  \
   2
    \
     3
      \
       4
        \
         5
          \
           6
            \
             7
              \
               8
                \
                 9  

671. Second Minimum Node In a Binary Tree ×

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Example 1:

Input: 
    2
   / \
  2   5
     / \
    5   7

Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2:

Input: 
    2
   / \
  2   2

Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

public int findSecondMinimumValue(TreeNode root) {
       if(root==null) return -1;
       if(root.left==null&&root.right==null) return -1;
       int leftVal = root.left.val;
       int rightVal = root.right.val;  
       if(root.val==leftVal) leftVal=findSecondMinimumValue(root.left);
       if(root.val==rightVal) rightVal=findSecondMinimumValue(root.right);
       if (leftVal != -1 && rightVal != -1) return Math.min(leftVal, rightVal);
       else return leftVal==-1?rightVal:leftVal;
   }

98. Validate Binary Search Tree -

• 中序遍历

  public boolean isValidBST(TreeNode root) {
      ArrayList<Integer> rec = new ArrayList();
      dfs(root,rec);
      for(int i=0;i<rec.size()-1;i++){
          if(rec.get(i)>=rec.get(i+1)) return false;
      }
      return true;
  }
  public void dfs(TreeNode root,ArrayList<Integer> rec){
      if(root==null) return;
      dfs(root.left,rec);
      rec.add(root.val);
      dfs(root.right,rec);
  }

• 递归

  public boolean isValidBST(TreeNode root) {
      return dfs(root,Long.MAX_VALUE,Long.MIN_VALUE);
  }
  public boolean dfs(TreeNode root,long max,long min){
      if(root==null) return true;
      if(root.val>=max||root.val<=min) return false;
      return dfs(root.left,root.val,min)&&dfs(root.right,max,root.val);
  }

110. Balanced Binary Tree √

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

Given the following tree [3,9,20,null,null,15,7]:

  3
 / \
9  20
  /  \
 15   7

Return true.

public boolean isBalanced(TreeNode root) {
       int rHeight=0,lHeight=0;
       if(root==null)
           return true;
       rHeight = checkHeight(root.right,rHeight);
       lHeight = checkHeight(root.left,lHeight);
       return Math.abs(rHeight-lHeight)<=1&&isBalanced(root.left)&&isBalanced(root.right);
   }
   public int checkHeight(TreeNode root,int height){
       if(root==null)
           return height;
       return 1+Math.max(checkHeight(root.right, height),checkHeight(root.left, height));

   }

两棵树的判断

101. Symmetric Tree √

Given a binary tree, check whether it is a mirror of itself (ie, symmetric around its center).

For example, this binary tree [1,2,2,3,4,4,3] is symmetric:

    1
   / \
  2   2
 / \ / \
3  4 4  3

But the following [1,2,2,null,3,null,3] is not:

  1
 / \
2   2
 \   \
 3    3

public boolean isSymmetric(TreeNode root) {
    if(root == null)
        return true;
    return checkSym(root.left,root.right);

}
public boolean checkSym(TreeNode p, TreeNode q){
    if(p==null&&q==null)
        return true;
    if(p==null||q==null)
        return false;
    return checkSym(p.left,q.right)&&checkSym(p.right,q.left)&&p.val==q.val;
}

100. Same Tree √

Given two binary trees, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical and the nodes have the same value.

Example 1:

Input:     1         1
          / \       / \
         2   3     2   3

        [1,2,3],   [1,2,3]

Output: true

Example 2:

Input:     1         1
          /           \
         2             2

        [1,2],     [1,null,2]

Output: false

Example 3:

Input:     1         1
          / \       / \
         2   1     1   2

        [1,2,1],   [1,1,2]

Output: false

public boolean isSameTree(TreeNode p, TreeNode q) { 
       if(p==null&&q==null) return true;
       if(p==null||q==null) return false;
       return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right)&&p.val==q.val;
   }

617. Merge Two Binary Trees √

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.

You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

Example 1:

Input: 
	Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
Output: 
Merged tree:
	     3
	    / \
	   4   5
	  / \   \ 
	 5   4   7

public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
       if(t1==null&&t2==null) return null;
       if(t1==null||t2==null) return t1==null?t2:t1;
       t1.val=t1.val+t2.val;
       t1.left=mergeTrees(t1.left,t2.left);
       t1.right=mergeTrees(t1.right,t2.right);
       return t1;
   }

572. Subtree of Another Tree √

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

    3
   / \
  4   5
 / \
1   2

Given tree t:

  4 
 / \
1   2

public boolean isSubtree(TreeNode s, TreeNode t) {
         if (s == null) return false;
        return isS(s,t)||isSubtree(s.left,t)||isSubtree(s.right,t);
    }
    public boolean isS(TreeNode s, TreeNode t){
        if(s==null&&t==null) return true;
        if(s==null||t==null) return false;       
        return t.val==s.val&&isS(s.left,t.left)&&isS(s.right,t.right);
    }